Codility Lesson 06

Lesson 6.1 - Distinct

Write a function

class Solution 
{
  public int solution(int[] A); 
}

that, given an array A consisting of N integers, returns the number of distinct values in array A.

For example, given array A consisting of six elements such that:

 A[0] = 2    A[1] = 1    A[2] = 1
 A[3] = 2    A[4] = 3    A[5] = 1

the function should return 3, because there are 3 distinct values appearing in array A, namely 1, 2 and 3.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [0..100,000];
• each element of array A is an integer within the range [−1,000,000..1,000,000].

using System;
using System.Linq;

/**
 * 6.1 - Distinct
 * Paulo Santos
 * 07.Dec.2022
 */
class Solution {
    public int solution(int[] A) {
        return A.Distinct().Count();
    }
}

---

Lesson 6.2 - Max Product of Three

A non-empty array A consisting of N integers is given. The product of triplet (P, Q, R) equates to A[P] * A[Q] * A[R] (0 ≤ P < Q < R < N).

For example, array A such that:

  A[0] = -3
  A[1] = 1
  A[2] = 2
  A[3] = -2
  A[4] = 5
  A[5] = 6

contains the following example triplets:

• (0, 1, 2), product is −3 * 1 * 2 = −6
• (1, 2, 4), product is 1 * 2 * 5 = 10
• (2, 4, 5), product is 2 * 5 * 6 = 60

Your goal is to find the maximal product of any triplet.

Write a function:

class Solution 
{
  public int solution(int[] A); 
}

that, given a non-empty array A, returns the value of the maximal product of any triplet.

For example, given array A such that:

  A[0] = -3
  A[1] = 1
  A[2] = 2
  A[3] = -2
  A[4] = 5
  A[5] = 6

the function should return 60, as the product of triplet (2, 4, 5) is maximal.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [3..100,000];
• each element of array A is an integer within the range [−1,000..1,000].

using System;

/**
 * 6.2 - Max Product of Three
 * Paulo Santos
 * 07.Dec.2022
 */
class Solution {
    public int solution(int[] A) {

        /*
         * Check the input
         */
        if (A == null)
            throw new ArgumentNullException();
        if (A.Length < 3)
            throw new ArgumentException();

        var min1 = int.MaxValue;
        var min2 = int.MaxValue;
        var max1 = int.MinValue;
        var max2 = int.MinValue;
        var max3 = int.MinValue;

        for (var i = 0; i < A.Length; i++) {
            /*
             * Get the two smallest numbers
             * in the array.
             */
            if (A[i] < min1) {
                min2 = min1;
                min1 = A[i];
            }
            else if (A[i] < min2) {
                min2 = A[i];
            }
            /*
             * Get the three largest numbers
             * in the array.
             */
            if (A[i] > max1) {
                max3 = max2;
                max2 = max1;
                max1 = A[i];
            } else if (A[i] > max2) {
                max3 = max2;
                max2 = A[i];
            } else if (A[i] > max3) {
                max3 = A[i];
            }
        }

        return Math.Max(min1 * min2 * max1, max1 * max2 * max3);

    }
}

---

6.3 - Triangle

An array A consisting of N integers is given. A triplet (P, Q, R) is triangular if 0 ≤ P < Q < R < N and:

A[P] + A[Q] > A[R],
A[Q] + A[R] > A[P],
A[R] + A[P] > A[Q].

For example, consider array A such that:

  A[0] = 10    A[1] = 2    A[2] = 5
  A[3] = 1     A[4] = 8    A[5] = 20

Triplet (0, 2, 4) is triangular.

Write a function:

class Solution 
{ 
  public int solution(int[] A); 
}

that, given an array A consisting of N integers, returns 1 if there exists a triangular triplet for this array and returns 0 otherwise.

For example, given array A such that:

  A[0] = 10    A[1] = 2    A[2] = 5
  A[3] = 1     A[4] = 8    A[5] = 20

the function should return 1, as explained above. Given array A such that:

  A[0] = 10    A[1] = 50    A[2] = 5
  A[3] = 1

the function should return 0.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [0..100,000];
• each element of array A is an integer within the range [−2,147,483,648..2,147,483,647].

using System;

/**
 * 6.3 - Triangle
 * Paulo Santos
 * 07.Dec.2022
 */
class Solution {
    public int solution(int[] A) {

        /*
         * Check inputs
         */
        if (A == null)
            throw new ArgumentNullException();
        if (A.Length < 3)
            return 0;
        
        /*
         * Sort the array
         */
        Array.Sort(A);

        /*
         * This way we only have to
         * deal with 3 consecutive
         * elements.
         */
        for (var i = 0; i < A.Length - 2; i++) {
            if ((((A[i]     + A[i + 1]) > A[i + 2]) &&
                 ((A[i + 1] + A[i + 2]) > A[i]    ) &&
                 ((A[i + 2] + A[i]    ) > A[i + 1])) ||
                 /*
                  * Deal with an outlier case when 
                  * there's a silent overflow on 
                  * the operations above
                  */
                 ((A[i]     == int.MaxValue) &&
                  (A[i]     == A[i + 1]    ) && 
                  (A[i + 1] == A[i + 2]    )))  {
                /*
                 * A triangle was found
                 */
                return 1;
            }
        }
        return 0;
    }
}

---

6.4 - Number of Disc Intersections

We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

  A[0] = 1
  A[1] = 5
  A[2] = 2
  A[3] = 1
  A[4] = 4
  A[5] = 0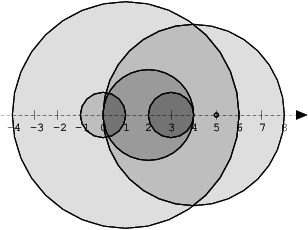

There are eleven (unordered) pairs of discs that intersect, namely:

• discs 1 and 4 intersect, and both intersect with all the other discs;
• disc 2 also intersects with discs 0 and 3.

Write a function:

class Solution 
{ 
  public int solution(int[] A); 
}

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Given array A shown above, the function should return 11, as explained above.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [0..100,000];
• each element of array A is an integer within the range [0..2,147,483,647].

using System;

/**
 * 6.4 - Number of Discs Intersercts
 * Paulo Santos
 * 07.Dec.2022
 */
class Solution {
    public int solution(int[] A) {

    int result = 0;
    var dps = new int[A.Length];
    var dpe = new int[A.Length];

    /*
     * Calculate start and finish
     * For the disks
     */
    for (int i = 0, x = A.Length - 1; i < A.Length; i++)
    {
        var s = (i > A[i])     ? i - A[i] : 0;
        var e = (x - i > A[i]) ? i + A[i] : x;
        dps[s]++; // Add overlap at the start
        dpe[e]++; // Add overlap ar the end
    }

    var t = 0;
    for (var i = 0; i < A.Length; i++)
    {
        /*
         * Does a circle starts 
         * at this position?
         */
        if (dps[i] > 0)
        {
            /*
             * Calculate the number
             * of overlaps
             */
            result += t * dps[i];
            result += dps[i] * (dps[i] - 1) / 2;

            /*
             * If the result is grater than 10,000,000
             * Return -1.
             */
            if (result > 10000000) 
                return -1;
            
            /*
             * Add the overlap to a 
             * temporary variable
             */
            t += dps[i];
        }
        t -= dpe[i];
    }

    return result;

    }
}