Codility Lesson 07

Lesson 7.1 - Brackets

A string S consisting of N characters is considered to be properly nested if any of the following conditions is true:

• S is empty;
• S has the form “(U)” or “[U]” or “{U}” where U is a properly nested string;
• S has the form “VW” where V and W are properly nested strings.

For example, the string “{[()()]}” is properly nested but “([)()]” is not.

Write a function:

class Solution 
{ 
  public int solution(String S); 
}

that, given a string S consisting of N characters, returns 1 if S is properly nested and 0 otherwise.

For example, given S = “{[()()]}”, the function should return 1 and given S = “([)()]”, the function should return 0, as explained above.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [0..200,000];
• string S is made only of the following characters: “(”, “{”, “[”, “]”, “}” and/or “)”.

using System;
using System.Collections.Generic;

/**
 * 7.1 - Brackets
 * Paulo Santos
 * 09.Dec.2022
 */
class Solution {

    const string bracketOpen  = "{[(";
    const string bracketClose = "}])";

    public int solution(string S) {

        var pos = 0;
        var isOpen = false;
        var bracketStack = new Stack<char>();

        foreach (var c in S) {
            if (!isOpen && (bracketClose.IndexOf(c) != -1)) 
                return 0;

            if (isOpen && (bracketClose.IndexOf(c) != -1)) {
                if (c != bracketStack.Peek()) 
                    return 0;

                bracketStack.Pop();
                isOpen = (bracketStack.Count != 0);
                continue;
            }
            if ((pos = bracketOpen.IndexOf(c)) != -1) {
                bracketStack.Push(bracketClose[pos]);
                isOpen = true;
            }
        }

        return (bracketStack.Count == 0) ? 1 : 0;

    }
}

---

7.2 - Fish

You are given two non-empty arrays A and B consisting of N integers. Arrays A and B represent N voracious fish in a river, ordered downstream along the flow of the river.

The fish are numbered from 0 to N − 1. If P and Q are two fish and P < Q, then fish P is initially upstream of fish Q. Initially, each fish has a unique position.

Fish number P is represented by A[P] and B[P]. Array A contains the sizes of the fish. All its elements are unique. Array B contains the directions of the fish. It contains only 0s and/or 1s, where:

• 0 represents a fish flowing upstream,
• 1 represents a fish flowing downstream.

If two fish move in opposite directions and there are no other (living) fish between them, they will eventually meet each other. Then only one fish can stay alive − the larger fish eats the smaller one. More precisely, we say that two fish P and Q meet each other when P < Q, B[P] = 1 and B[Q] = 0, and there are no living fish between them. After they meet:

• If A[P] > A[Q] then P eats Q, and P will still be flowing downstream,
• If A[Q] > A[P] then Q eats P, and Q will still be flowing upstream.

We assume that all the fish are flowing at the same speed. That is, fish moving in the same direction never meet. The goal is to calculate the number of fish that will stay alive.

For example, consider arrays A and B such that:

  A[0] = 4    B[0] = 0
  A[1] = 3    B[1] = 1
  A[2] = 2    B[2] = 0
  A[3] = 1    B[3] = 0
  A[4] = 5    B[4] = 0

Initially all the fish are alive and all except fish number 1 are moving upstream. Fish number 1 meets fish number 2 and eats it, then it meets fish number 3 and eats it too. Finally, it meets fish number 4 and is eaten by it. The remaining two fish, number 0 and 4, never meet and therefore stay alive.

Write a function:

class Solution 
{
  public int solution(int[] A, int[] B); 
}

that, given two non-empty arrays A and B consisting of N integers, returns the number of fish that will stay alive.

For example, given the arrays shown above, the function should return 2, as explained above.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [1..100,000];
• each element of array A is an integer within the range [0..1,000,000,000];
• each element of array B is an integer that can have one of the following values: 0, 1;
• the elements of A are all distinct.

using System;
using System.Collections.Generic;

/**
 * 7.2 - Fish
 * Paulo Santos
 * 09.Dec.2022
 */
class Solution {

    private class Fish {

        public Fish(int s, int d) {
            this.Size = s;
            this.Direction = d;
        }

        public int Size      {get; private set;}
        public int Direction {get; private set;}
    }

    public int solution(int[] A, int[] B) {

        var sEats = new Stack<Fish>();

        sEats.Push(new Fish(A[0], B[0]));
        for (var i = 1; i < A.Length; i++) {
            if (sEats.Peek().Direction == B[i]) {
                /*
                 * Add to the stack
                 */
                sEats.Push(new Fish(A[i], B[i]));
                continue;
            }

            /*
             * If the top fist is flowing upstream
             * it's not the right condition to see
             * who's eating who.
             */
            if (sEats.Peek().Direction == 0) {
                sEats.Push(new Fish(A[i], B[i]));
            }
            else {
                /*
                 * Figure out who's eating who
                 */
                while (sEats.Count > 0) {
                    /*
                     * Top fish swimming in the same direction
                     * They can't eat each other
                     */
                    if (sEats.Peek().Direction == B[i]) {
                        sEats.Push(new Fish(A[i], B[i]));
                        break;
                    }
                    else {
                        /*
                         * Top fish eats current fish?
                         */
                        if (sEats.Peek().Size > A[i]) {
                            /*
                             * yes.
                             */
                            break;
                        }
                        else {
                            /*
                             * nope.
                             */
                            sEats.Pop();
                            continue;
                        }
                    }
                }
                if (sEats.Count == 0) {
                    sEats.Push(new Fish(A[i], B[i]));
                }
            }
        }

        return sEats.Count;
    }
}

---

7.3 - Nesting

A string S consisting of N characters is called properly nested if:

• S is empty;
• S has the form “(U)” where U is a properly nested string;
• S has the form “VW” where V and W are properly nested strings.

For example, string “(()(())())” is properly nested but string “())” isn’t.

Write a function:

class Solution 
{
  public int solution(String S); 
}

that, given a string S consisting of N characters, returns 1 if string S is properly nested and 0 otherwise.

For example, given S = “(()(())())”, the function should return 1 and given S = “())”, the function should return 0, as explained above.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [0..1,000,000];
• string S is made only of the characters “(” and/or “)”.

using System;

/**
 * 7.3 - Nesting
 * Paulo Santos
 * 09.Dec.2022
 */
class Solution {
    public int solution(string S) {
        
        /*
         * I don't usually editorialize on this
         * lessons, but this one I had to.
         *
         * Lesson 7.3 is ridiculously similar to 7.1
         * 
         * Just saying.
         */
        
        var cnt = 0;
        var isOpen = false;
        foreach(var c in S) {
            if (c == ')') {
                if (!isOpen)
                    return 0;

                cnt -= 1;
                isOpen = (cnt > 0);
                continue;
            }
            if (c == '(') {
                cnt += 1;
                isOpen = true;
            } 
        }

        return (cnt == 0) ? 1 : 0;
    }
}

---

7.4 - Stonewall

You are going to build a stone wall. The wall should be straight and N meters long, and its thickness should be constant; however, it should have different heights in different places. The height of the wall is specified by an array H of N positive integers. H[I] is the height of the wall from I to I+1 meters to the right of its left end. In particular, H[0] is the height of the wall's left end and H[N−1] is the height of the wall's right end.

The wall should be built of cuboid stone blocks (that is, all sides of such blocks are rectangular). Your task is to compute the minimum number of blocks needed to build the wall.

Write a function:

class Solution 
{
  public int solution(int[] H); 
}

that, given an array H of N positive integers specifying the height of the wall, returns the minimum number of blocks needed to build it.

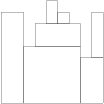
For example, given array H containing N = 9 integers:

  H[0] = 8    H[1] = 8    H[2] = 5
  H[3] = 7    H[4] = 9    H[5] = 8
  H[6] = 7    H[7] = 4    H[8] = 8

the function should return 7. The figure shows one possible arrangement of seven blocks.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [1..100,000];
• each element of array H is an integer within the range [1..1,000,000,000].

using System;
using System.Collections.Generic;

/**
 * 7.4 - Stonewall
 * Paulo Santos
 * 09.Dec.2022
 */
class Solution {
    public int solution(int[] H) {

        /*
         * Number of blocks
         */
        var lst = new List<Tuple<int, int>>();

        /*
         * The start of the wall
         */
        var blk = new Tuple<int, int>(0, H[0]);
        var stk = new Stack<Tuple<int, int>>();

        lst.Add(blk);
        stk.Push(blk);

        for(var i = 1; i < H.Length; i++) {
            /*
             * Check if the stack of
             * blocks has the same height 
             * of the wall
             */
            if (H[i] == stk.Peek().Item2) 
                continue;
            
            /*
             * Is it's height greater?
             */
            if (H[i] > stk.Peek().Item2) {
                /*
                 * Add another block
                 */
                blk = new Tuple<int, int>(stk.Peek().Item2, H[i]);
                lst.Add(blk);
                stk.Push(blk);
                continue;
            }

            /*
             * It's smaller. 
             * Go through the stack to see
             * If we can find a smaller block
             */
            blk = null;
            stk.Pop();
            while (stk.Count > 0) {
                if (H[i] == stk.Peek().Item2)
                {
                    blk = stk.Peek();
                    break;
                }
                if (H[i] > stk.Peek().Item2) {
                    blk = new Tuple<int, int>(stk.Peek().Item2, H[i]);
                    lst.Add(blk);
                    break;
                }
                stk.Pop();
            }

            if (blk == null) {
                blk = new Tuple<int, int>(0, H[i]);
                lst.Add(blk);
            }

            stk.Push(blk);
        }

        return lst.Count;
    }
}